Making Robots Move Naturally: Our Whole-Body Controller for Holistic Mobile Manipulators

Why We Need Better Robot Movement

Picture a robot trying to pick up objects while moving around. Current robots typically do this in a clunky way - first they drive somewhere, come to a complete stop, and only then start reaching for things. It's like they can't walk and reach at the same time! This makes them slow and inefficient at many everyday tasks.

We tackled this problem by building a system that helps robots move more fluidly. Our solution uses some pretty cool tech - VAMP (Vectorized Autonomous Motion Planning)[1] and multilayer RRTC[2] - to figure out smooth paths that let the robot's wheels and arm work together. But having a good plan is only half the battle - the robot needs to actually follow that plan accurately.

That's where our controller comes in, and it's what we'll focus on in this article. While working on our system, we found that existing robot controllers just weren't up to the task. They were great at moving either the wheels or the arm, but not both at once. So we created our own controller that could handle this complex coordination - keeping the wheels and arm moving together smoothly, just like they do in our plans.

1. Limitations of Traditional Control Approaches

Before examining our solution, let's analyze why conventional control approaches are insufficient for coordinated whole-body motion:

1.1 PD Control Limitations

Most robotic systems rely on PD (Proportional-Derivative) controllers for trajectory tracking. While effective for single-component control, these controllers have several significant limitations for whole-body coordination:

• Discontinuous motion profiles: The controllers produce abrupt acceleration changes, resulting in inefficient and imprecise movement patterns.
• Limited trajectory tracking: They struggle with complex curved paths, particularly when coordinating multiple degrees of freedom.
• Reactive-only behavior: The lack of predictive capability limits their effectiveness in dynamic environments and coordinated movements.

Consider a standard PD controller with sampling period (\(\Delta t\)) attempting to follow a pose trajectory (\(x_{ref}(t)\)) without velocity information:

When following a trajectory defined only by discrete positions (\(x_{ref}(t_k)\)) at fixed intervals, the controller faces several mathematical challenges:

Velocity Estimation Error: Without explicit trajectory velocities, the controller must estimate velocity from consecutive position goals:

$\dot{x}_{est}(t_k) = \frac{x_{ref}(t_k) - x_{ref}(t_{k-1})}{\Delta t}$

This estimation introduces significant quantization errors, especially for complex trajectories with varying curvatures.

Transient Response Limitations: For a standard second-order system under PD control, the minimum settling time is bounded by:

$t_s \geq \frac{4}{\zeta \omega_n}$

where (\(\zeta\)) is the damping ratio and (\(\omega_n\)) is the natural frequency. For fixed gains (\(K_p\)) and (\(K_d\)), this creates a fundamental trade-off between speed and overshooting that cannot be circumvented.

These limitations become particularly problematic when attempting to coordinate multiple degrees of freedom simultaneously, especially when the robot has a noisy localization system and big impedance mismatch between the arm and the base.

1.2 Separate Controllers: The "Left Hand Doesn't Know What the Right Is Doing" Problem

Another common approach is to use entirely separate controllers for the arm and base. This is like having two different people controlling different parts of the robot without talking to each other. As you might imagine, this leads to problems:

• Coordination nightmares: Getting the timing right between arm and base movements is incredibly tricky.
• Wasted motion: Without considering how the whole system works together, movements are often inefficient or awkward.
• Sequential instead of simultaneous: The robot tends to move in stages rather than flowing naturally from one action to the next.

2. Our Whole-Body Controller

Our approach builds on Model Predictive Control (MPC), which has become a standard technique in mobile robot navigation. In the navigation domain, MPC is widely used as both a local planner and controller, leveraging optimization solvers to generate trajectories that are smooth, feasible, and safe while keeping velocities within hardware constraints.

While MPC has been successfully deployed in numerous open-source navigation solutions, these implementations typically focus solely on base motion. We extend this paradigm to encompass whole-body control, simultaneously coordinating the mobile base, torso, and manipulator arm through a unified optimization framework.

2.1 State and Control Definitions

We formulate the problem by defining the complete state vector for the mobile manipulator:

2.2 System Dynamics Model

Our controller implements a discrete-time kinematic model to predict future states based on current state and control inputs. Since the mobile base is non-holonomic (i.e., it cannot move sideways directly), the state transition equations must respect these constraints:

The discrete state update equation then becomes:

Where (\(s_k\)) represents slack variables that slightly relax the dynamics constraints. These slack variables are crucial for computational tractability in real-time applications, allowing the optimizer to find feasible solutions even when perfect dynamics satisfaction would be challenging due to discretization errors or model simplifications.

In our implementation, this dynamics constraint is formulated as:

for i in range(self.N):
    x = X[:,i]
    u = U[:,i]
    
    dx = ca.vertcat(
        u[0] * ca.cos(x[2]),  # x
        u[0] * ca.sin(x[2]),  # y
        u[1],                 # theta
        u[2],                 # torso
        u[3:]                 # arm joints
    )
    
    # Relax dynamics constraints with slack variables
    opti.subject_to(X[:,i+1] == x + dx * self.dt + slack_dynamics[:,i])
        

This formulation allows the controller to project the robot's state evolution over a finite prediction horizon while accounting for the non-holonomic constraints of the mobile base, enabling coordinated whole-body motion planning.

2.3 Optimization Problem Formulation

The MPC controller optimizes a quadratic cost function over the prediction horizon while satisfying various constraints:

This objective function balances four competing criteria:

1. Tracking error minimization (weighted by positive definite matrix \(Q\))
2. Control effort efficiency (weighted by positive definite matrix \(R\))
3. Dynamics constraint satisfaction (penalized by \(\alpha_1\))
4. Safety constraint satisfaction (penalized by \(\alpha_2\))

The optimization is subject to several constraints:

# Input constraints
for i in range(self.N):
    # Linear velocity
    opti.subject_to(U[0,i] <= self.max_linear_vel)
    opti.subject_to(U[0,i] >= -self.max_linear_vel)
    
    # Angular velocity
    opti.subject_to(U[1,i] <= self.max_angular_vel)
    opti.subject_to(U[1,i] >= -self.max_angular_vel)
    
    # Torso and arm joint velocities
    for j in range(self.n_torso_joints + self.n_arm_joints):
        opti.subject_to(U[2+j,i] <= self.max_joint_vel[j])
        opti.subject_to(U[2+j,i] >= -self.max_joint_vel[j])

# Non-negativity constraints for slack variables
opti.subject_to(opti.bounded(0, slack_dynamics, 1.0))

# Initial state constraint (no slack)
opti.subject_to(X[:,0] == X0)

These constraints ensure that:

• Control inputs remain within hardware limits
• Slack variables are bounded to prevent excessive constraint violation
• The initial state matches the current robot state exactly

3. Obstacle Avoidance with Control Barrier Functions

While our whole-body motion planner generates collision-free trajectories through sampling-based methods, we still need robust collision avoidance in the controller. This is because sampling-based planners may generate trajectories that, while technically collision-free, can be dangerous in practice. For example, the planner might generate paths that:

• Pass close to obstacles: Moving very close to a table corner or along a wall might be collision-free in theory, but becomes risky when accounting for localization errors or tracking inaccuracies
• Have minimal clearance: The planned path might maintain just enough distance to avoid collision, leaving no margin for real-world uncertainties
• Assume perfect execution: The planner doesn't account for controller tracking errors or dynamic obstacles

To address these challenges, we implement Control Barrier Functions (CBFs) within our optimization framework. CBFs provide a mathematically rigorous way to enforce safety constraints while maintaining smooth motion, effectively creating a safety buffer around obstacles that adapts to the robot's movement.

3.1 Barrier Function Theory

A Control Barrier Function is a tool from nonlinear control theory that transforms safety constraints into forward-invariant sets. For a dynamical system with state (\(x\)) and control input (\(u\)), a CBF is defined through a continuously differentiable function (\(h: \mathbb{R}^n \rightarrow \mathbb{R}\)) where the safe set is described as:

The key property of a CBF is that if (\(h(x) \geq 0\)) initially, then the system can be controlled to ensure (\(h(x) \geq 0\)) for all future time. This is achieved by enforcing the following condition:

Where (\(\gamma > 0\)) is a tuning parameter that determines how aggressively the system maintains safety. This continuous-time condition translates to our discrete-time MPC setting as:

3.2 CBF Formulation for Obstacle Avoidance

For mobile robot navigation, we define the barrier function for each obstacle as:

This formulation has several advantageous properties:

• Differentiable everywhere, making it suitable for gradient-based optimization
• Radially symmetric, providing uniform safety margins around obstacles
• Computationally efficient to evaluate and differentiate
• Natural interpretation: positive values indicate safe distances, negative values indicate constraint violation

3.3 Relaxed CBF Constraints

In practice, we implement a relaxed version of the CBF constraints using slack variables to ensure optimization feasibility:

The slack variables (\(s_{cbf}\)) are penalized in the objective function with weight (\(\alpha_2\)):

This formulation provides several key benefits:

• Guaranteed feasibility of the optimization problem
• Smooth degradation of safety constraints when necessary
• Tunable trade-off between safety and performance via (\(\alpha_2\))
• Ability to handle multiple obstacles with different priorities

3.4 Efficient Obstacle Processing

A critical challenge in implementing CBF-based collision avoidance is processing real-world sensor data efficiently. Our robot uses a 2D LIDAR sensor that provides hundreds of obstacle points per scan. Including all these points as constraints would make the optimization problem computationally intractable for real-time control. We solve this through an efficient voxelization approach:

1. Data Collection: Raw LIDAR scans are processed at 5Hz, independent of the 10Hz control loop, to maintain real-time performance
2. Voxel Grid Filtering: The 2D space is divided into a grid of voxels (0.2m × 0.2m), and points within each voxel are represented by their centroid
3. Proximity-Based Selection: Voxel centroids are sorted by distance to the robot, and only the 10 nearest obstacles are included in the optimization

This processing pipeline is implemented as follows:

# Group points into voxels using a dictionary for efficiency
voxel_dict = {}
for x, y in points_map:
    voxel_x = int(x / voxel_size)
    voxel_y = int(y / voxel_size)
    voxel_key = (voxel_x, voxel_y)
    if voxel_key not in voxel_dict:
        voxel_dict[voxel_key] = []
    voxel_dict[voxel_key].append((x, y))

# Calculate centroid of each voxel
obstacle_positions = []
for voxel_points in voxel_dict.values():
    x_sum = sum(p[0] for p in voxel_points)
    y_sum = sum(p[1] for p in voxel_points)
    count = len(voxel_points)
    centroid = (x_sum / count, y_sum / count)
    obstacle_positions.append(centroid)

# Sort by distance to robot and keep closest N
obstacle_positions.sort(key=lambda p: 
    (p[0] - robot_x)**2 + (p[1] - robot_y)**2)
obstacle_positions = obstacle_positions[:max_obstacle_points]

This approach provides several benefits:

• Computational Efficiency: Reduces hundreds of LIDAR points to a manageable set of constraints
• Spatial Coverage: Voxelization ensures obstacles are represented across the entire sensor range
• Dynamic Updates: Processing runs in a separate thread, allowing continuous obstacle tracking without impacting control performance

3.5 Implementation Details

The CBF constraints are implemented with careful consideration of numerical stability and computational efficiency:

def h(x_, y_):
    return (x_[0] - y_[0])**2 + (x_[1] - y_[1])**2 - self.safe_distance**2

# Add CBF constraints for each obstacle
for j in range(self.max_obstacle_points):
    for i in range(self.M_CBF):
        # Current and next state positions
        robot_curr = X[:2, i]
        robot_next = X[:2, i+1]
        
        # Get obstacle positions from parameter array
        obs_curr_x = obstacle_params[0, j*(self.N+1) + i]
        obs_curr_y = obstacle_params[1, j*(self.N+1) + i]
        obs_next_x = obstacle_params[0, j*(self.N+1) + i+1]
        obs_next_y = obstacle_params[1, j*(self.N+1) + i+1]
        
        obs_curr = ca.vertcat(obs_curr_x, obs_curr_y)
        obs_next = ca.vertcat(obs_next_x, obs_next_y)
        
        # Add CBF constraint with slack
        opti.subject_to(
            h(robot_next, obs_next) >= 
            (1 - self.gamma_k) * h(robot_curr, obs_curr) - cbf_slack[j, i]
        )

Key implementation considerations include:

• Efficient vectorization of constraints using CasADi's symbolic framework
• Separate slack variables for each obstacle and timestep to allow fine-grained constraint relaxation
• Prediction of obstacle motion to maintain safety margins during dynamic scenarios
• Gradual decay rate (\(\gamma_k\)) to prevent aggressive avoidance maneuvers

3.6 Theoretical Guarantees

The CBF formulation provides several important theoretical guarantees:

• Forward Invariance: If the initial state is safe and (\(s_{cbf} = 0\)), the system remains safe for all future time
• Lipschitz Continuity: The barrier function's gradients are bounded, ensuring numerical stability
• Recursive Feasibility: If a solution exists at time k, a solution will exist at time k+1 (with slack variables)
• Minimal Conservatism: The constraints only activate when necessary, allowing optimal performance in safe regions

The complete optimization problem is solved using IPOPT with the following configuration:

# Set solver options
opts = {
    'ipopt.print_level': 0 if not self.debug else 3,
    'print_time': 0 if not self.debug else 1,
    'ipopt.max_iter': 100,
    'ipopt.tol': 1e-4,
    'ipopt.acceptable_tol': 1e-3,
    'ipopt.acceptable_obj_change_tol': 1e-4,
    'ipopt.warm_start_init_point': 'yes'
}

# Create and call the solver
self.opti.solver('ipopt', opts)

The solver is configured to balance computational efficiency with solution quality, using warm starts to improve convergence speed in subsequent iterations.

4. Implementation Results

Our implementation achieves real-time performance with a 10Hz control loop, where each MPC optimization takes approximately 70ms to solve. Below is a demonstration of our controller in action:

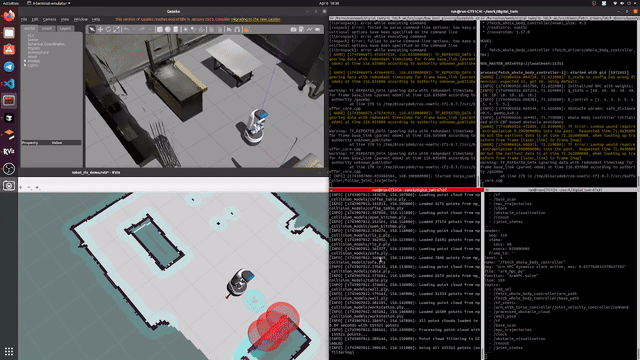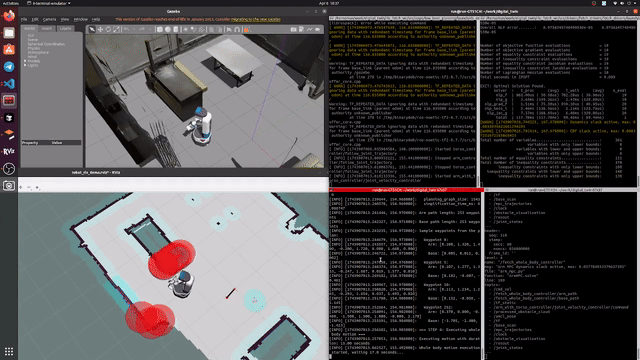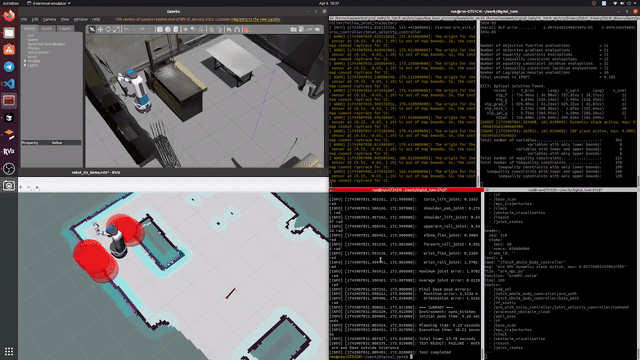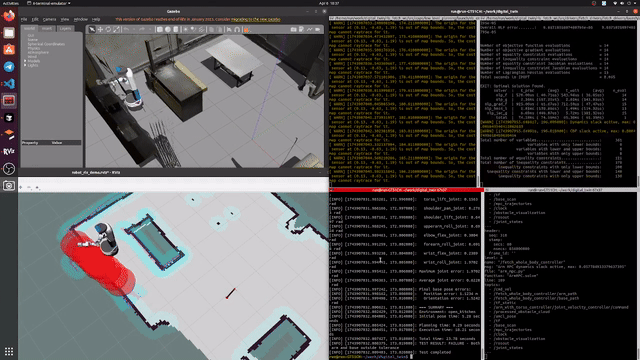
Figure 1: Real-time demonstration of our whole-body MPC controller (8x playback speed). The robot performs coordinated base and arm motions while maintaining safe distances from obstacles, represented by red circles (voxel centroids). Note how the controller smoothly adjusts the robot's trajectory to maintain safety margins around detected obstacles.

5. Conclusion

This work demonstrates how mathematical rigor and practical engineering can come together to solve a fundamental robotics challenge. By combining MPC with control barrier functions, we showed that robots can move more naturally and safely, breaking free from the traditional stop-and-go paradigm. The key insight is that complex robotic behaviors don't always need complex solutions - sometimes they just need the right mathematical framework and careful implementation.

Our open-source implementation runs at 10Hz on standard hardware, showing that advanced control techniques are becoming increasingly practical for real-world applications. We hope this work inspires others to push the boundaries of robot control, making robots more capable partners in our daily lives.

  @misc{whole-body-mpc,
    author    = {Author Name},
    title     = {Unified Whole-Body MPC Controller for Mobile Manipulators},
    year      = {2025},
    publisher = {GitHub},
    url       = {https://h-tr.github.io/blog/posts/mpc-whole-body-control.html}
  }